المحتويات
حل الصفحة 23 من رياضيات اول ثانوي التمرين رقم 77 :
هل تبحث عن حل تمرين 77 ص 23 من كتاب رياضيات 1 ثانوي؟ أنت في المكان الصحيح على منصة فيرال تجد الاجابة على هذا التمرين وتمارين أخرى، فقد لاحظنا مؤخرًا أن هناك الكثير من عناوين البحث حول حل تمارين مختلفة خاصة في الرياضيات ومساقات اخرى من خلال شبكات ومواقع مختلفة ، على سبيل المثال هذا التمرين “حل تمرين 77 ص 23 رياضيات 1 ثانوي؟” ، لذلك في هذه المقالة سوف نُطلعكم على الحل والنتيجة الصحيحة لهذا التمرين.
حل تمرين 77 ص 23 رياضيات 1 ثانوي؟
حل تمرين 77 ص 23 رياضيات 1 ثانوي؟
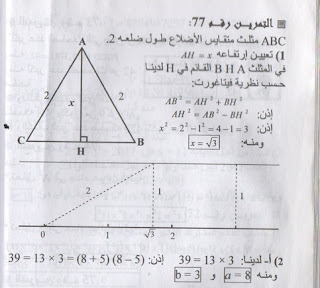
الإجابة على التمرين موضحة في الصورة:
حيث أن السؤال مطروح عن مثلث ABC متقايس الأضلاع طول ضلعه 2.
ومطلوب من الطالب حساب نظرية فيثاغورت.
الجدير بالذكر هنا، أن نظرية فيثاغورس هي علاقة أساسية في الهندسة الإقليدية بين أضلاع المثلث قائم الزّاوية. تنص على أنّ مجموع مربعي طولي ضلعي الزاوية القائمة مساوٍ لمربع طول الوتر. يُمكن كتابة النّظرية كمعادلة تربط بين أطوال أضلاع المثلث ا ب جـ. سميت هذه المبرهنة هكذا نسبةً إلى العالم فيثاغورس الذي كان رياضياً وفيلسوفاً وعالم فلك في اليونان القديمة.
نظرية فيثاغورس المباشرة
وهي الشكل الأكثر شهرة لنظرية فيثاغورس:
« في مثلث قائم الزاوية، مربع طول الوتر يساوي مجموع مربعي طولي الضلعين المحاذيين للزاوية القائمة. »

في مثلث ABC قائم الزاوية في C، أي أن [AB] هو الوتر، نضع AB=c و AC=b و BC=a. لدينا:
أو
تمكن نظرية فيثاغورس من حساب طول أحد أضلاع مثلث قائم الزاوية بمعرفة طولي الضلعين الآخرين. مثلا: إذا كان b=3 و a=4 فإن
ومنه 
أي ثلاثة أعداد صحيحة تمثل أطوال أضلاع مثلث قائم الزاوية -مثل (3، 4، 5)- تُكون ثلاثي فيثاغورسي.


